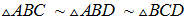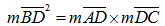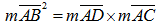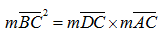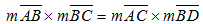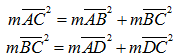A) Mesures de longueur dans un même cercle
1. Toute médiatrice à une corde (d'un cercle) détermine un diamètre.
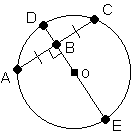B est le point milieu de AC.
DE passe par B et est perpendiculaire à AC.
Alors, DE est la médiatrice de la corde AC.
Donc :
DE est un diamètre du cercle de centre O.
2. La plus grande corde d'un cercle est un diamètre.
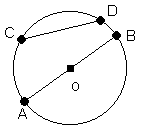La corde AB est un diamètre car elle passe par le centre du cercle.
Donc :
La corde AB est plus grande que la corde CD, qui elle, n’est pas un diamètre.
3. Dans un cercle, tout rayon perpendiculaire à une corde partage cette corde en deux segments congrus.
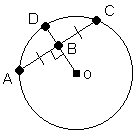Le rayon OD est perpendiculaire à la corde AC.
Il coupe cette corde au point B.
Donc :
Les segments AB et BC sont congrus.
4. Dans un cercle, tout rayon perpendiculaire à une corde partage l'arc qu'elle sous-tend en deux arcs congrus.
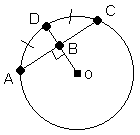Le rayon OD est perpendiculaire à la corde AC.
La corde AC sous-tend l'arc ADC.
Donc :
Les arcs AD et DC sont congrus.
5. Dans un cercle, des arcs compris entre deux cordes parallèles sont congrus.
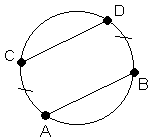Les cordes AB et CD sont parallèles.
Les arcs AB et BD sont compris entre ces deux cordes parallèles.
Donc :
Les arcs AC et BD sont congrus.
6. Deux cordes situées à une même distance du centre d'un cercle sont congrues.
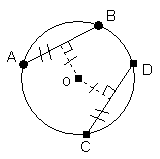La distance entre le centre O du cercle et la corde AB
et
la distance entre le centre O et la code CD est la même.
Donc :
Les cordes AB et CD sont congrues.
7. Dans un cercle, des cordes congrues sous-tendent des arcs congrus et, réciproquement, des arcs congrus sont sous-tendus par des cordes congrues.
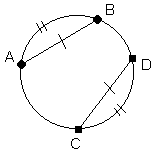Les cordes AB et CD sont congrues.
Donc :
Les arcs que ces cordes sous-tendent,
i.e. les arcs AB et CD sont congrus aussi.
Les arcs AB et CD sont congrus.
Donc:
Les cordes AB et CD le sont aussi.
8. Toute tangente à un cercle est perpendiculaire au rayon qui aboutit au point de tangence.
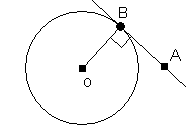La droite AB est tangente au cercle en un point B.
Donc :
La tangente AB est perpendiculaire au rayon OB.
9. Deux tangentes à un cercle issues d'un même point extérieur au cercle déterminent des segments congrus. (Les segments sont mesurés entre le point duquel les tangentes sont issues et chacun des points de tangence.)
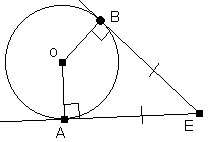EA et EB sont 2 tangentes au cercle issues d’un point extérieur E.
Donc :
EA et EB sont congrus.
10. Deux droites parallèles, sécantes ou tangentes à un cercle, interceptent sur ce cercle, entre les deux droites parallèles, des arcs congrus.
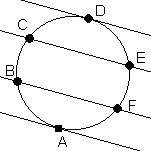Les droites D, CE, BF et A sont parallèles.
Donc :
Chaque paire d’arcs interceptée par deux de ces droites est congrue.
Par exemple, les arcs AC et AE sont congrus.
B) Rapports entre les mesures de deux cercles
11. Le rapport des circonférences de deux cercles et celui des mesures de leur rayon respectif forment une proportion.
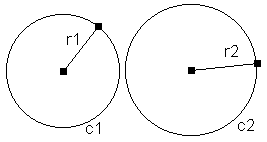c1 et c2 représentent les circonférences des cercles et r1 et r2, leurs rayons.
Donc :
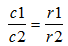
12. Le rapport des aires de deux cercles et celui du carré des mesures de leur rayon respectif forment une proportion.
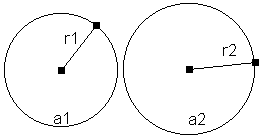a1 et a2 représentent les aires des cercles et r1 et r2, leurs rayons.
Donc :
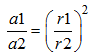
13. Le rapport des mesures des arcs semblables de deux cercles et celui des mesures de leur rayon respectif forment une proportion.
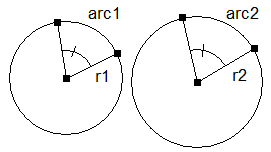L'arc 1 a la même mesure que l'arc 2.
Donc :
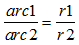
C) Mesures d'angles dans un même cercle
14. Dans un cercle, la mesure d'un angle au centre est égale à la mesure de l'arc intercepté par ses côtés.
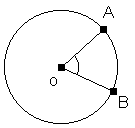L'angle AOB est un angle au centre
car O est le centre du cercle.
Donc :
La mesure de l'arc AB est la même que la mesure de l'angle AOB.
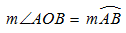
15. Dans un cercle, la mesure d'un angle inscrit est égale à la demi-mesure de l'arc intercepté par ses côtés.
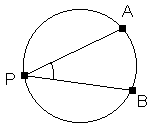L'angle APB est un angle inscrit
car P est un point situé sur le cercle.
L'arc AB est l'arc intercepté par les côtés de l'angle APB.
Donc :
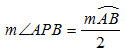
16. La mesure d'un angle dont le sommet est situé à l'intérieur d'un cercle est égale à la demi-somme des mesures des arcs interceptés par les côtés de l'angle et par leurs prolongements.
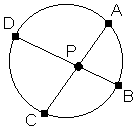Les angles APB et CPD sont congrus car ils sont opposés par le sommet P.
Ce sommet est situé à l'intérieur d'un cercle.
Donc :
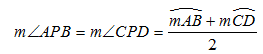
17. La mesure d'un angle dont le sommet est situé à l'extérieur d'un cercle est égale à la demi-différence entre les mesures des arcs interceptés par les côtés de l'angle.
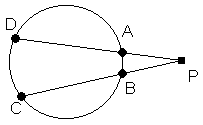L'angle APB (ou DPC) a son sommet en un point P situé à l'extérieur d'un cercle.
Les côtés de cet angle interceptent les arcs CD et AB sur ce cercle.
Donc :
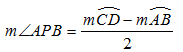
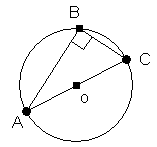Le triangle ABC, rectangle en B, est inscrit dans le cercle de centre O.
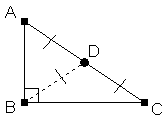AC est l’hypoténuse car c’est le côté opposé à l’angle droit. BD est la médiane relative à l’hypoténuse AC car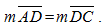 
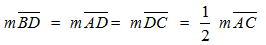
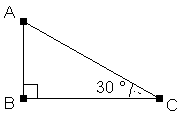L’angle C mesure 30°. Le côté AB est opposé à cet angle. Le côté AC est l’hypoténuse car il est opposé à l’angle droit.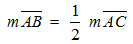
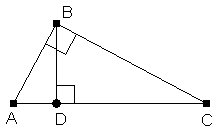Soit ABC, le triangle rectangle initial et les triangles ABD et BCD formés par la hauteur BD relative à l’hypoténuse AC.
Haut de la page