Voici la dernière phrase du 3e paragraphe :
La Lune est aussi attirée par la Terre est c'est pourquoi elle tourne autour sans s'en éloigner.
En fait, la Lune s'éloigne de quelques centimètres par année de la Terre. Voir ces paragraphes sur l'éloignement lunaire.
Sur le schéma a), allongez de 2 carreaux vers la droite la longueur du trait indiquant la longueur d'onde, puis remplacer les mots Longueur d'onde par Période.
Ne pas considérer les petites bosses qui cachent les roues de la bicyclette.
Dans certaines versions du manuel, le corrigé ne montre pas la trajectoire correcte pour la partie (a).
Le corrigé mentionne que le graphique ne représente pas une onde sonore mais la variation de pression de l'air autour de la source sonore.
En fait, nous avons bien la représentation d'une onde sonore à une position précise dans l'espace en fonction du temps.
En effet, le graphique ne représente pas l'onde à un moment précis en fonction de sa position dans l'espace, comme par exemple, à la figure 1.14. Dans ce cas, la longueur d'onde est la distance mesurée selon l'axe des x entre deux crêtes ou deux creux d'ondes successives.
Le corrigé deviendrait :
Le graphique représente bien une onde sonore à une position précise dans l'espace en fonction du temps. Il ne représente pas l'onde à un moment précis dans le temps en fonction de sa position dans l'espace.
Tel que dessiné sur le schéma, la longueur du pendule est plus petite dans la position du centre, comparée aux 2 autres positions.
Sur le schéma, allongez la longueur du pendule lorsque celui-ci est représentée en position centrale.
Sur la rose des vents, le symbole "N" apparaît pour "Nord" et pour "Ouest".
Sur la rose des vents, à l'ouest, remplacer "N" par "O".
À la page 2.38, en utilisant l'échelle proposée, le tracé des vecteurs va se retrouver au-delà de la partie quadrillée du plan cartésien.
Déplacer l'axe 'Ouest-Est' de 3 carreaux vers le bas.
Dans le graphique,
remplacer Rx = 13 par Ry = 13
remplacer Ry = -5 par Rx = -5
Dans le dessin du corrigé, intervertir 12h et 14h.
Dans l'énoncé de la question, remplacer
Voici ses déplacements par rapport à la station ...
par
Voici ses déplacements successifs à partir de la station ...
Dans le dessin du corrigé, la flèche du vecteur
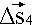pointe vers le nord de l'ouest alors qu'elle devrait pointer vers le sud de l'est.
Note : La correction a été effectuée à la réédition de juin 2004.
À la figure 3.9, remplacer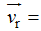 
6,2 km/h par 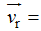6,32 km/h.
À la 4e ligne de [ 3.32 ],
remplacer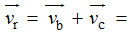 
6,2 km/h ... par 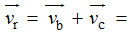6,32 km/h ...
Le problème ne peut pas être résolu car il manque une information.
Ajouter après l'énoncé du problème, avant les questions :
Grâce à cette manoeuvre, le bateau franchit la rivière selon une trajectoire perpendiculaire aux deux rives.
Le corrigé donne un vecteur vitesse de 168 km/h à 66° au nord de l'est.
Un calcul précis donne plutôt 170,9 km/h à 65,6° au nord de l'est.
La question mentionne que l'avion pointe son nez vers le sud. Cependant, sur le dessin qui semble représenter le tableau de bord de l'avion, le nez de l'avion pointe en direction nord-est.
Ne pas tenir compte du dessin de l'avion.
L'énoncé du problème fait référence aux graphiques A et B de l'exercice 4.4 situé à la page [ 4.16 ]. Considérons ces deux graphiques qui représentent les vitesses en fonction du temps de deux mobiles. Le graphique A s'arrête à un temps de 4 secondes sur l'axe des "x". Le graphique B s'arrête à 8 secondes.
Dans le corrigé de l'exercice 4.10 situé à la page [ C.74 ], le graphique de l'accélération des deux mobiles en fonction du temps s'arrêtent à 5.5 secondes sur l'axe des "x".
Logiquement, le graphique de l'accélération en fonction du temps correspondant au graphique A devrait s'arrêter à 4 secondes et le celui correspondant au graphique B devrait s'arrêter à 8 secondes.
À la fin de la 2e ligne, dans le corrigé, remplacer :
v = -18 km/h par v = -180 km/h
À la [ figure 4.16 de 4.62 ], on indique bien que la vitesse de descente est 180 km/h.
Selon le texte qui précède ce graphique, chaque point sur le graphique représente la position de la balle à un moment donné. L'axe des « x » ne représente pas un temps en secondes mais plutôt la distance horizontale parcourue en mètres, l'axe des « y » représente la distance verticale parcourue en mètres. Le point le plus à gauche représente la position de la balle au temps t = 0 seconde. Les autres points représentent les positions de la balle à tous les 1/30 de seconde.
Donc les axes des « x » et des « y » sont en mètres, le temps étant défini comme un paramètre du graphique.
Dans le bas du graphique, remplaçons la définition de l'axe des « x » :
Temps (s) par Position horizontale (m).
De même, à gauche du graphique, précisons la définition de l'axe des « y » et remplaçons :
Position (m) par Position verticale (m).
Une fois corrigé selon les indications situées plus haut sur cette page, le graphique de la page [ 5.12 ] est similaire à celui de la page [ 5.19 ]. La différence, c'est qu'à la page [ 5.19 ], on a voulu obtenir une meilleure résolution sur l'axe des « y » représentant la position verticale.
Cependant, il y a une erreur sur la graduation de l'échelle des « y ». En haut, à gauche du graphe, on a placé la valeur 1,2 (m), ce qui donne un écart de 0,2 m pour la dernière graduation (1,2 - 1,0) alors que l'écart est de 0,1 m pour toutes les graduations précédentes.
À cause de cela, le graphique n'est pas acceptable et l'allure de la demi-parabole représentant la trajectoire de la balle n'est pas régulière. Il y a une légère réorientation de la trajection à la position horizontale x = 0,4 m.
En conclusion, ne pas utilisez le graphique de la page [ 5.19 ]. Corrigez plutôt le graphique de la page [ 5.12 ] selon les indications situées plus haut et utilisez ce dernier.
Le manuel indique :
• pour le mouvement horizontal :
- vitesse : ...
- position : x = vi t = ...
Remplacer : x = vi t = ... par x = vx t = ...
À la dernière ligne, le corrigé indique :
« La portée du canon est de 29,5 km. »
Remplacer par :
La portée du canon est de 25,5 km.
Note : La correction a été effectuée à la réédition de juin 2004.
Voici la 5e ligne du corrigé : vyf2 = 235,2 m3/s2
Remplacer par : vyf2 = 235,2 m2/s2
Considérant l'orientation de l'angle, remplacer 66°, la valeur de l'angle, par -66°.
Corriger les lignes suivantes.
Note : La correction a été effectuée à la réédition de juin 2004.
L'énoncé 4 est le suivant :
4. Vous observez qu’une voiture est en mouvement parce qu’elle change de position par rapport à une borne-fontaine. Tout autre objet aurait pu faire l’affaire.
Cet énoncé est classé parmi les énoncés vrais. Il serait bon d'ajouter une précision :
Tout autre objet fixe par rapport au sol sur lequel se déplace la voiture aurait pu faire l’affaire.
En effet, si la voiture change de position par rapport à un nuage qui se déplace dans le ciel, il est possible que la voiture ne se déplace pas par rapport à l’observateur.
Une vitesse de 166 km/h correspond à 46,1 m/s et non à 40 m/s.
Dans le corrigé, la seconde partie du graphique (de 0,6 s à 1,0 s) montre une vitesse de 40 m/s. Il faut modifier le graphique pour désigner une vitesse de 46,1 m/s.
Note : La correction a été effectuée à la réédition de juin 2004.
Dans le corrigé, remplacer la 4e et la 5e ligne de la page C.125, par :
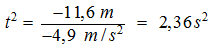et donc t = 1,54 s
Temps total = 0,65 s + 1,54 s = 2,19 s.
Note : La correction a été effectuée à la réédition de juin 2004.
Haut de la page